One challenge in building analytical models involves separating signal from noise. Signal describes the patterns we consider “real” in the sense that we believe they reflect a true relationship between the factors we’re analyzing. For instance, if our data indicates that a person’s height is related to her weight, we’d probably consider that signal.
Noise, on the other hand, describes patterns present only in the subset of the data we’re examining, and we wouldn’t expect them to continue beyond that. So, if our data tells us that a person’s height is related to her first initial, we’re probably picking up on noise.
Separating Signal from Noise
In predictive analytical models, we hope that basing our models on signal variables will lead to higher accuracy. This consideration invariably leads us to split our data into a training set and a validation set. We feed the training set to our algorithm to detect patterns and fit a model. We then use that model to predict the target values of the validation set we withheld and compare the predicted values to the recorded values. We repeat the process, finally settling on the model whose predictions come the closest:

Above: Comparing the actual recorded values to the values our model predicted
The idea is this: if we give our algorithm all the data we have, we get a model optimized to “predict” the target values we already have. But that’s not what we want. Instead, we want to optimize our model to predict values we do not already have. So, we withhold a part of our data and force the algorithm to select those model variations that work well on this “unknown” data. That, we hope, will drive the algorithm to use signal variables in fitting the model:

Above: Breaking up our dataset into training data (used to build different models) and validation data (used to evaluate those models). In most instances, the validation set should be a randomized sample.
Identifying Signal with Cross-Validation
Splitting into training and validation, though, doesn’t eliminate the risk of incorporating noise variables as predictors (also called overfitting). Sure, we’re optimizing a model to predict “unknown” data, but it’s still the same dataset over and over, so we’re building a model that’s optimized to predict a specific subset of our data.
Cross-validation, in response, takes it one step further. Instead of splitting our data into training and validation sets once at the beginning, we go through several rounds, each time re-shuffling and re-splitting our data:
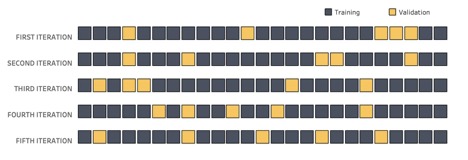
Above: In cross-validation, we go through multiple rounds of model-building, each time drawing a new validation set.
A variation of this practice is called k-fold cross-validation, in which we split our data into a specific number of subsets, or folds, and use a different fold as the validation set in each round:
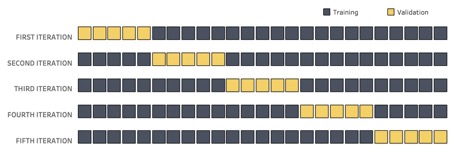
Above: K-fold cross-validation involves splitting our data into several folds, each of which will serve as the validation set for one the model-building rounds
By using these cross-validation methods, we end up with a final model that is a composite of all the models that worked best on all the different validation sets. This approach, while resource-intensive, significantly reduces the risk of overfitting and enhances our ability to create robust, accurate, signal-based models.
What This All Means
Whenever we’re building predictive models, we want to make sure we’re picking up on the underlying truth of the data, rather than the randomness inherent to it. Cross-validation methods are a powerful tool to achieve that end without having to collect additional data, and models built using cross-validation are better equipped to make accurate predictions on unknown data.

