Relying on p-values to reach business decisions is common, which is reason for concern. Conducting analysis that’s too heavily based on p-values and engages in an unfettered quest for statistical significance can lead to decisions that are fundamentally unsound. To understand why, we’re going to go all the way back to Ancient Greece.
Reductio Ad Absurdum
Aristotle came up with a fantastic way of evaluating the truth of a claim: you momentarily accept the claim as true and see if doing so causes any problems. It’s called reductio ad absurdum, Latin for reduction to absurdity.
For instance, let’s suppose my friend claims that her commute is only a five-minute drive in her car. One way to evaluate this claim is to take it as true and examine the consequences of doing so. We can determine the distance between my friend’s home and her workplace and figure out how fast she’d have to drive in a straight line to make the trip in five minutes. If that number turns out to be, say, 300 miles per hour, and her car has a top speed of only 120 miles per hour, I can safely call out my friend’s statement as nonsense.
After all, if the claim implies that her commute is only five minutes long because she routinely drives her car in excess of 300 miles per hour (even though it has a top speed of 120 miles per hour), that’s “absurd.” Therefore, her claim is false. Reductio!

Reductio Ad Unlikely
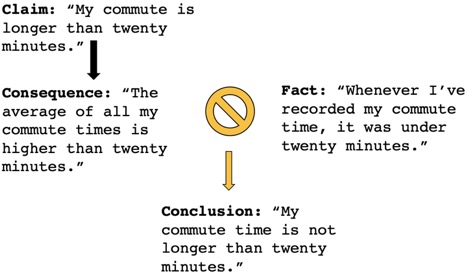
Statisticians employ something similar to the reductio ad absurdum when they evaluate hypotheses. Let’s suppose I wanted to know how long my morning commute was. I have a pretty strong feeling that it’s longer than 20 minutes, but I want to know for sure. So, tomorrow morning, I time myself door-to-door and clock in at 18 minutes. Done! Eighteen is not larger than 20, so I can reject the claim that it takes longer than twenty minutes for me to get to work. Right?
In this kind of scenario, we should worry that my one-time recording of an 18-minute commute may have been a fluke. For all we know, my true commute time is 25 minutes, and it just happened to be unusually short the day I measured it, perhaps due to low traffic or excellent visibility.
Fine, I might say: I can just time my commutes for the entire week, average them all out and see if that average is larger or smaller than 20. But maybe the whole week turns out to be a fluke, too; maybe I happen to pick the one week with good road conditions, and any other week would have been all snowstorms and black ice. I could keep timing myself and taking averages over longer and longer time spans, but in a strictly logical sense, I’ll never be sure that the times I’m recording reflect my true commute time.
Accounting for Potential Flukes
In statistics, we approach the problem that our measurements could be a fluke by quantifying the likelihood that they are, in fact, a fluke. Just as in the reductio ad absurdum, we first assume (temporarily) the truth of our claim: my commute time is longer than 20 minutes. We then compare this to the average commute time I recorded, 18 minutes.
Now, in the classical reductio ad absurdum, we would ask whether it is possible that (a) my true commute time is over 20 minutes, and (b) I recorded a number of commutes that averaged out to 18 minutes. And yes, of course it is! But in statistics, we put a spin on the reductio. Assuming that my true commute time is over 20 minutes, what is the probability that I recorded a number of commutes that averaged out to 18 minutes? Statisticians admit that sure, it’s possible that my true commute time is longer than 20 minutes, but they ask whether it is likely. And if it’s very unlikely that I record an 18-minute commute when my commute is actually longer than 20 minutes, statisticians go ahead and say that my commute isn’t longer than 20 minutes. Reductio-ish!
Possibility vs. Probability
We call this probability the p-value: the probability that, assuming our hypothesis is true (my true commute time is longer than 20 minutes), I still recorded an average commute time of 18 minutes. By nothing but convention, many scientists reject hypotheses at a p-value of less than 0.05, or five percent: if it turns out that recording an average commute time of 18 minutes would only happen five percent of the time in a world where my true commute time is over 20 minutes, we’re comfortable saying that my true commute isn’t longer than 20 minutes. In his wonderful book How Not To Be Wrong: The Power Of Mathematical Thinking, Jordan Ellenberg calls this the reductio ad unlikely:
The Thing About p-Values
If this sounds fishy, it is! After all, Aristotle’s reductio ad absurdum tells us that a claim is false to a logical certainty. My friend’s commute cannot possibly be only five minutes long. And the reductio ad unlikely merely tells us that a claim is probably false. My commute is unlikely to be longer than 20 minutes. That’s disappointing. Then again, we constantly make decisions based on probability and rarely have perfect information.
That goes for science, too: If we fail to poke holes in a hypothesis, we say that it’s probably true and accept it for now, but we subject it to revision if we discover new evidence or a better theory. The conclusions we draw in our daily lives, in science and in business are often just the educated guesses we make based on the information available to us, and we seem to be largely okay with that.
The Improbability Principle
But there is a real peril with this approach: unlikely things happen all the time. The mathematics professor David J. Hand calls this the “improbability principle.” A roulette ball lands on black 26 times in a row. A girl releases a balloon that is caught 140 miles away by another girl with the same name. The same person wins the same lottery twice with the same numbers. If we operate on probability, we’re bound to sometimes reject claims that are perfectly true. “Unlike its Aristotelian ancestor,” Ellenberg writes, “the reductio ad unlikely is not logically sound in general.”
The American Statistical Association (ASA) agrees, releasing a statement in 2016 meant to “steer research into a post p<0.05 era.” In it, the ASA stresses “[t]he p-value was never intended to be a substitute for scientific reasoning.” What that era looks like, exactly, hasn’t fully revealed itself, and it certainly hasn’t arrived.
What This Means for You
For now, it’s fine to consider p-values in reaching decisions or to use them as a starting point. But it’s important to resist the urge to use p-values as the arbiter of truth because doing so equates what is improbable to what is impossible.
For those interested, here are some of the sources mentioned in this post for further exploration:


